Rooftop solar estimate

We want to compare this to the capacity were the panels mounted on the roof of the building. The shape of the building is somewhat similar to the following

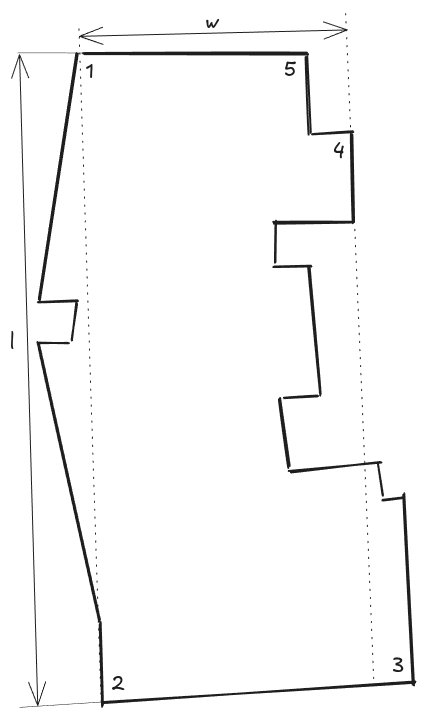
In the leading picture of this post we are looking at the buildings' upper left corner (1->3 direction).

First we shall estimate the width $w$ of the building. As can be seen in the picture above the wide wall harbours two windows. It's also possible to distinguish that each floor consists of 3 apparently quadratic blocks, with windows being present in only two of those. Oh the beauty of the LPS design.

Because of the apparently quadratic shape we can estimate the width of each block via the floors height. The lowest estimate that seems reasonable is around \( 2.5[m] \) since people with a height of \( \sim 2[m] \) are not uncommon and should thus be able to live without scraping the their head on the ceiling in such a building. The upper estimate that still appears reasonable would be around \(4[m]\). It is an even number that would allow even the tallest person (except for world-record outliers) to be able to stretch inside, but it seems to me an estimate that leaves a lot of vertical space unused - hence it is the upper limit. Our estimate will thus be the geometric mean of both:

$$h_{floor} = \sqrt{2.5\cdot 4}[m]\approx 3.16 [m]\;.$$

This height seems reasonable as an approximation but unwieldy in construction where one would, naively, expect dimensions to be provided to a full or half-metre. Thus we may decide to round the estimate down to

$$h_{floor} := 3[m]$$

Alternative derivation

We can estimate the width of one block indirectly by way of estimating how wide a window is and how many windows could be squeezed, side-by-side, into the block.

First, in a way similar to the above, we can estimate the width of a window on the side of the building. From the vantage point in the picture the windows look like they could fit at least 1 1/2 humans side-by-side and at most 3. With an average shoulder width of around 50 cm this would correspond to a window width of between \(0.75[m]\) and \(1.5[m]\).

Applying the same procedure as above we get

$$w_{window} = \sqrt{0.75 \cdot 1.5}\approx 1.06 [m]$$

Next we can estimate how many windows could be squeezed into the width of a single block of the wall. It appears that 2 windows could be fit comfortably into the same width, but 5 would be already stretching the boundaries of belief. Hence:

$$N_{windows} = \sqrt{2\cdot 5} \approx 3.16\;.$$

Using this estimate we obtain a second estimate of the width of a single block (and hence the height of the floor):

$$w_{block} = 3.16\cdot 1.06[m] \approx 3.35 [m]\;.$$

The estimate is close to our direct estimate of \(3.16 [m]\) improving the confidence in our estimates. With the same reasoning as above we hence estimate the width of a building block to be

$$w_{block} := 3 [m]\;.$$

Building width

This gives us an estimated length of the visible wall of \(3\cdot 3[m]=9[m]\). An additional section not visible in the picture but shown in the sketch is present, which is ~1 plate wide. Thus the overall width of the building is around

$$w = 4\cdot h_{floor} = 12 [m]$$

Building length

Next we estimate the length \(l\) of the building, again via multiple steps.

Our first estimate of the length will be using the visible building width, which was computed in Building width. By way of visual comparison we can estimate that the building is at least 3 times and at most 5 times longer than the visible width. This yields an estimated length

$$l_{est} = \sqrt{3\cdot 5} \cdot 9 [m]\approx 34.85 [m]\rightarrow 35[m]$$

Next we derive the length estimate from estimating the window dimensions for the balconies and the remainder on the right. We observe that each balcony consists of two windows and a door. Both windows are split in a roughly 2:1 configuration, for a total width of 3 units. The slimmest section being one unit we estimate its width at around 1 to 1.5 persons, or 50 to 75 cm with a geometric average being \(\sqrt{0.375}\approx 0.61 [m]\). This yields the width of the window to be \(3 \cdot 0.61 \approx 1.83 [m]\). There being two of them per balcony results in the width of the balcony being at least \(3.66 [m]\). Additionally we can estimate the door to be a bit wider than the slim section of the window and thus estimate its width at \(1 [m]\), resulting in an overall length of a balcony being \(4.66 [m]\), which we can fairly safely round up to \(5 [m]\) on the basis that we have neglected wall thickness and that this would be a much more likely width for a construction site!

We can see 5 balconies per floor. They do not cover the entire extent of the building. Hence the minimal length of the building is larger than \(25 [m]\).

Separating the two sets of visible balconies is a wall covering the stairwell. In the image it appears to be roughly as wide as one wide window, or \(1.83 [m]\). We note that a stairs must be wide enough for two people to comfortably pass each other. Hence the stairwell, being two pairs of stairs wide, must be wide enough to fit at least 4 people side-by-side and will generally be a bit wider. Thus we estimate the width at \(5\) people, or \(5\cdot 0.5 [m] = 2.5 [m]\). We have obtained two estimates that are notably different. If we compute their mean (arithmetic or geometric) the resulting estimate will be on the order of \(2.1 [m]\), or at most 4 persons wide. Since this seems to be too narrow we shall stick with the larger estimate of \(2.5[m]\).

Finally, the rightmost part of the building consists of a solid wall. Its length is unknown but it appears to be somewhere between 1 and 3 balconies long. Thus \(\sqrt{1\cdot 3}\approx 1.73\) balconies, or \(8.66 [m]\).

In total we thus reach an estimated length of the building

$$5\cdot 5[m] + 2.5 [m] + 8.66[m] = 36.16 [m]$$

This is fairly close to our estimate using only the visible width of the building, resulting in a \(3\%\) error.

---

We are thus approximating the shape of the building by a rectangle of dimensions \(\sim 36[m] \times \sim 12[m]\), resulting in a rooftop area of \(432 [m^2]\). A solar panel's area is roughly \(2m^2\), with its long side being \(\approx 2[m]\) and the short side being \(\approx 1[m]\) . This allows us to deck out the roof in \(216\) panels, with each clocking in at \(500 [W]\) and thus for a peak of \(108 [kW]\).

In a first instance, thus, we estimate that the capacity of balcony solar is \(\approx 65\%\) that of the rooftop for this building! This is comparing apples and oranges, though, since both installations are governed by different laws and the rooftop solar installation would require more extensive permitting. In an ideal case a building would carry both a rooftop solar array and balcony solar, which would turn it into a power station with up to \(190 [kW]\) peak power generation capacity.