Validating the estimate

Before proceeding with the next steps we shall validate our results to help calibrate the "gut feeling" required for estimates. The estimate of the peak power of balcony solar was fairly straightforward and does not require additional verification. The estimation of the capacity of a rooftop installation consists of multiple consecutive estimates and thus requires verification. For this we shall use www.openstreetmap.org and https://gps-coordinates.org/distance-between-coordinates.php .

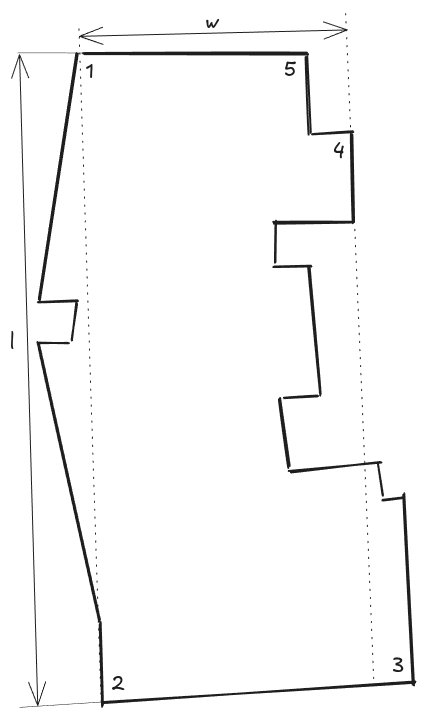
From the first one we shall take the corner coordinates of the building

Corner	Latitude	Longitude
1	50.1546399	8.6856246
2	50.1542744	8.6858640
3	50.1543533	8.6860966
4	50.1546566	8.6858394
5	50.1546793	8.6857860

Using corners 1 & 2 yields a distance of \(44.08 [m]\) which is noticeably higher than our estimate of \(36.16 [m]\)!

Using corners 1 & 5 we obtain a distance of \(12.31 [m]\), while using corners 2 & 3 provides us a limit on the effective building width of \(18.75[m]\). An arithmetic average yields a mean width of \(15.53 [m]\). Which is larger than our estimate of \(12 [m]\) by approx. 22%.

We may use the additional coordinate point \( (50.1543462, 8.6858229) \) in conjunction with corner 2 to determine the length of the rightmost wall without balconies. The calculation yields \(8.5[m]\), which is fairly close to our estimate of \(8.66 [m]\).

Given the calculated mean length and width of the building we can calculate the surface area of the roof to be

$$12.31 \times 44.08 = 542.6 [m^2]\;.$$

Our estimate is \(432 [m^2]\) and thus deviates from the GPS-based estimate by 25%! Since the power estimate relates to the area estimate in a linear fashion our peak rooftop power estimate will be too small, too. From the validation we obtain a peak rooftop solar estimate of

$$\frac{542.6 [m^2]}{2[m^2]}\cdot 500[W] = 135650 = 135.6 [kW]$$

resulting in difference of \( 27.6 [kW]\).